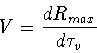| |
(24) |
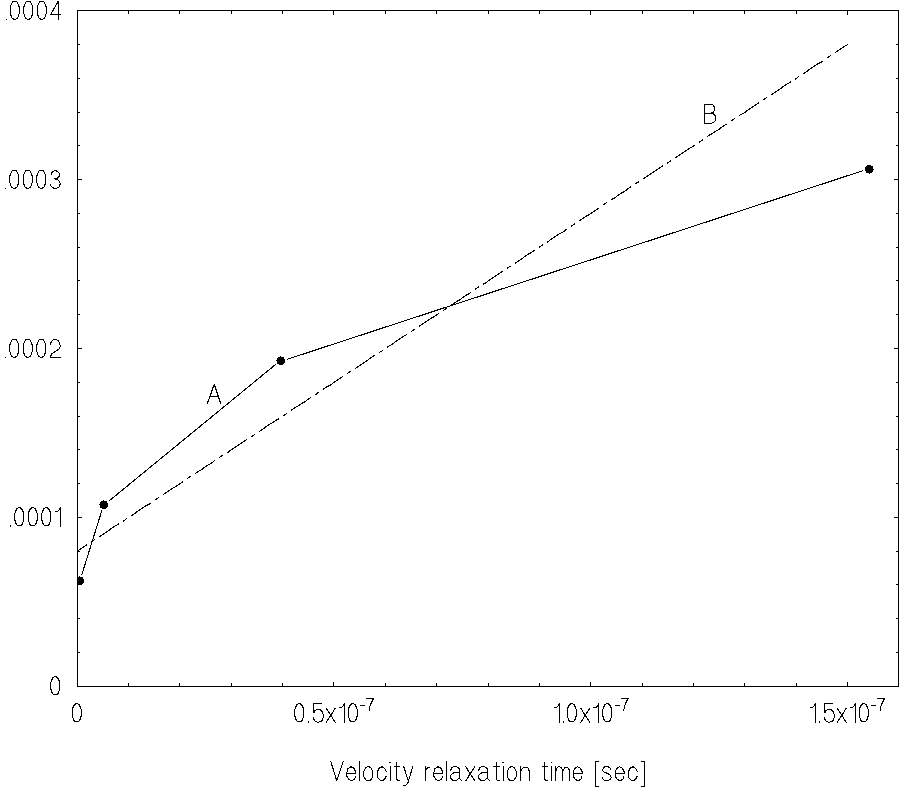
Fig.4 shows the muonium formation rate n(t) in superfluid helium
over the temperature range
The muonium formation rate increases for time interval
![]() with decreasing helium temperature and the rate
decreases for time
with decreasing helium temperature and the rate
decreases for time
![]() .
It is interesting to compare these
results with the measurements of muonium precession amplitude published
in paper [13], which makes it clear that the
decreasing of AMu at large temperature results from the formation time
.
It is interesting to compare these
results with the measurements of muonium precession amplitude published
in paper [13], which makes it clear that the
decreasing of AMu at large temperature results from the formation time
Let us consider the function W(r) which is radial density distribution
of muon-electron pairs. This function makes obvious physical sense for
the Coulomb attraction of a muon and an electron in liquid helium in the
viscous regime. This distribution function is appropriate when the ions
have relaxed to their final local equilibrium and their relative velocity
vector will be
We will ignore for simplicity the space asymmetry of distribution function
W(r), which was discovered in paper [14]. Then we obtain
the equation
It can easily be shown that the velocity relaxation time
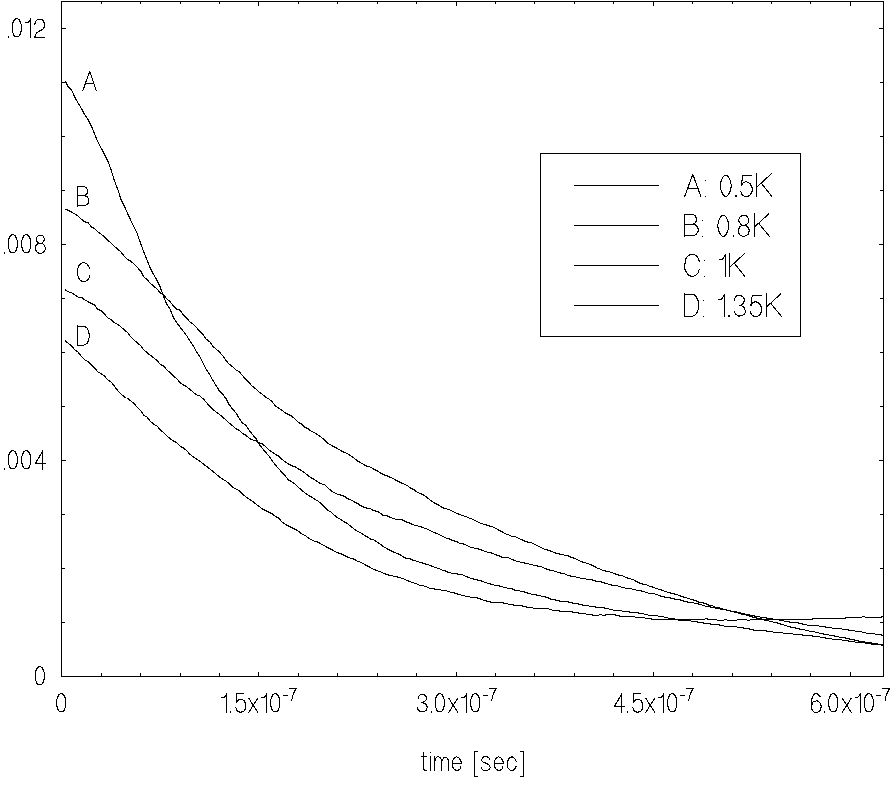
It is seen from this figure
that both the mean and the dispersion of the distance between muon and
electron pairs increase as the helium temperature is reduced.
This follows by virtue of increasing mobility for particles in superfluid
helium. The thermalization process in normal liquids are completed by a
time of 10-12 to 10-10 s because of elastic phonon interactions.
In contrast there is a gap
![]() in the superfluid helium
excitation spectrum [15] which results in an anomalously high mobility
of impurity particles, such as muons. As the energy of particles is reduced
to less than 8K, the velocity relaxation time
in the superfluid helium
excitation spectrum [15] which results in an anomalously high mobility
of impurity particles, such as muons. As the energy of particles is reduced
to less than 8K, the velocity relaxation time ![]() rises greatly.
The positions of the maximums in the Fig.5 correspond to mean distances
between muon and electron and their displacement is determined by
dispersion of particles over the time
rises greatly.
The positions of the maximums in the Fig.5 correspond to mean distances
between muon and electron and their displacement is determined by
dispersion of particles over the time ![]() .
.
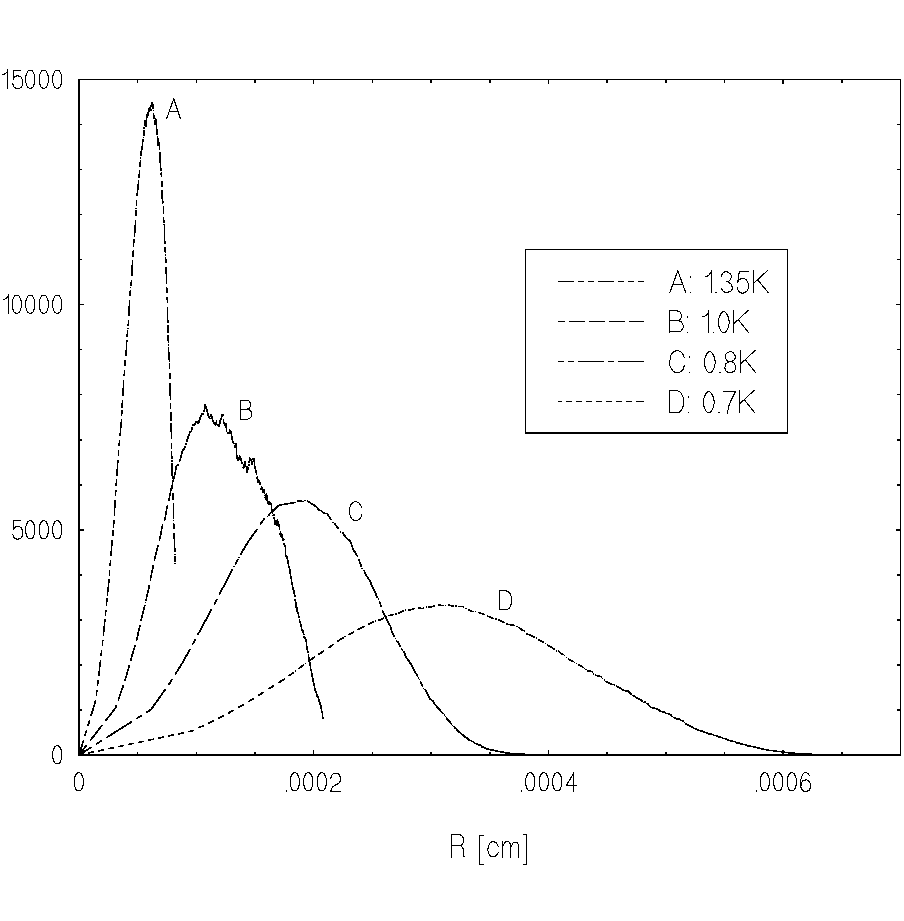
The dependence of the mean distance Rmax on the relaxation time ![]() is presented in Fig.6. It is seen from the figure that dispersion speed
is presented in Fig.6. It is seen from the figure that dispersion speed